 Il Decibel
Il Decibel
Storia, definizioni ed utilizzo di una (apparentemente) strana unità di misura
a cura di Giacomo Scalzo – Spring s.r.l.
Introduzione
Chiunque lavori nel campo dell’elettronica, della fisica, dell’acustica, delle telecomunicazioni su rame, su fibra ottica o su portante radio, ma anche in numerosi altri campi della tecnica, prima o poi si imbatte in grandezze espresse in dB (decibel), o suoi diretti derivati. È un metodo talmente diffuso per rappresentare il comportamento di un sistema che, per lo meno il suo simbolo, è diventato familiare ad una larghissima schiera di tecnici che lo utilizzano quotidianamente per esprimere il risultato di una misura, le caratteristiche di un prodotto, la valutazione di un’operazione di installazione, le prestazioni di un apparato, ecc.
Purtroppo non a tutti è altrettanto chiaro il concetto che sta alla base delle misurazioni in decibel e di conseguenza viene spesso a mancare la sensibilità necessaria per capire con immediatezza il significato fisico di ciò che si sta misurando. È sempre presente in questi casi il rischio di sovrastimare o sottovalutare una condizione marginale o di non saper confrontare correttamente le prestazioni di soluzioni alternative. Per esempio, tutti sono in grado di comprendere cosa significa se affermo che un certo cavo in fibra ottica attenua di 500 volte il segnale in ingresso, ma se affermassi che un secondo cavo attenua di 30dB, quanti sarebbero in grado di stimarne, anche in modo approssimativo, il comportamento? È migliore o peggiore del primo? E tra un cavo che attenua il segnale, per esempio, di 25 dB e un altro che presenta un’attenuazione di 28 dB che rapporto c’è? Di quanto il secondo è effettivamente peggiore del primo?
Ho fatto, volutamente, due esempi molto semplici: se sapete rispondere a queste domande forse potete anche passare alla lettura di un altro articolo, ma se non siete in grado di rispondere immediatamente, allora vi consiglio di continuare a leggere.
La trattazione che segue si pone semplicemente lo scopo di permettere al lettore di prendere confidenza con questa strana unità di misura quel tanto che basta per utilizzarla correttamente e con consapevolezza nei campi di applicazione trattati da questa rivista; chi volesse approfondire i concetti appresi o studiarne l’applicazione in altri settori d’elezione (l’acustica, per esempio) non farà certamente fatica a rintracciare numerosissime altre fonti di informazione.
Perchè il decibel
La prima cosa che è necessario puntualizzare è che la scala in decibel nasce per rappresentare un rapporto tra due grandezze fisiche. Rapporto significa che la grandezza non è misurata in valore assoluto ma sempre in modo relativo, riferita ad un’altra, in un altro punto del sistema o sotto diverse condizioni. Per esempio la potenza (elettrica, ottica, sonora, ecc.) in uscita da un sistema rapportata a quella in ingresso: siccome la grandezza in uscita può essere maggiore o minore di quella in ingresso, quello che si esprime con questo rapporto non è altro che il guadagno o l’attenuazione introdotto dal sistema preso in considerazione.
In termini pratici, se parliamo di potenze e se indico questo rapporto come Pu/Pi, si ha che:
- quando la potenza di uscita è più grande di quella in ingresso, cioè Pu > Pi (amplificazione) avremo Pu/Pi > 1
- quando la potenza di uscita è più piccola di quella in ingresso, cioè Pu < Pi (attenuazione) allora avremo Pu/Pi < 1
- quando la potenza di uscita è esattamente uguale a quella in ingresso, cioè Pu = Pi, allora il sistema né amplifica né attenua e Pu/Pi = 1
Un’altra considerazione importante è che questo rapporto (proprio perché è un rapporto), è adimensionale, cioè non rappresenta una grandezza fisica ma è un numero puro.
Il decibel non è altro che un metodo per rappresentare questo rapporto ma utilizzando una scala logaritmica invece che lineare. Il vantaggio di utilizzare una scala logaritmica è legato a diversi fattori ma per le applicazioni di nostro interesse, basterà citare la praticità che deriva dal fatto di manipolare numeri sempre relativamente piccoli e la facilità con cui si può calcolare il comportamento di un sistema anche particolarmente complesso a partire dai suoi elementi costitutivi.

Figura 1 – Esempio di grafico con scala delle ordinate lineare
Facciamo ancora qualche esempio: in Figura 1 abbiamo riportato un grafico che riporta come sono evolute nel tempo le applicazioni di rete su cavo in rame.
La scala utilizzata per i valori riportati sull’asse verticale è lineare. Il grafico è praticamente illeggibile, perché la necessità di inserire il punto 10 Gb/s, praticamente “schiaccia” tutta la zona da 0 a 1Gb/s estremamente importante, invece, per un’analisi dal punto di vista storico. Lo stesso grafico con la scala dell’asse verticale in formato logaritmico, Figura 2, mette in evidenza molto bene tutti i passi evolutivi (occorre solo prestare attenzione a come lo si “legge”, due punti che sembrano ad altezza doppia l’uno

Figura 2 – Esempio di grafico con scale delle ordinate logaritmica
rispetto all’altro, non rappresentano valori di prestazioni doppie, così come due punti apparentemente vicini possono rappresentare sistemi con comportamento molto diverso!).
In questo caso la scala logaritmica ci aiuta perché siamo in presenza di un sistema ad elevata dinamica, come si dice in gergo tecnico, cioè caratterizzato da valori che spaziano su un campo di variabilità molto grande, pari a più ordini di grandezza; riprenderemo più avanti questo punto facendo altri esempi, ora torniamo al nostro decibel.
La necessità di un sistema di misura con queste caratteristiche è nata all’inizio del secolo scorso, con la comparsa dei primi impianti telefonici. Più precisamente, trattandosi di impianti che avevano un ”segnale” sia in entrata che in uscita, si è sentito il bisogno di trovare il modo di misurare la qualità della comunicazione dal confronto di questi segnali.
Originariamente veniva utilizzato il MSC, Miles of Standard Cable: 1 MSC corrisponde alla perdita di potenza lungo 1 miglio di cavo telefonico standard alla frequenza di 800 Hz. L’utilizzo di un’unità che dipendesse dal tipo di cavo e dalla frequenza non permetteva particolari generalizzazioni, considerando anche che la definizione di cavo standard cambiava in funzione del Paese in cui avveniva la misura (non esistevano ancora standard internazionali). Gli ingegneri dei Bell Telephone Laboratories, i pionieri dell’ingegneria delle telecomunicazioni, fissarono quindi la TU, Telecommunication Unit: un’unità di misura che esprime quanto una grandezza è relativamente più grande rispetto ad un determinato livello. Operativamente la TU viene definita come: “dieci volte il logaritmo del rapporto tra le due quantità prese in considerazione”. Agli inizi degli anni ’20 questa definizione verrà ripresa per la definizione di Bel (in omaggio al fondatore dei Laboratories, Alexander Graham Bell), multiplo del più famoso ed utilizzato decibel.
Utilizziamo il decibel
Il decibel quindi è stato introdotto per rappresentare un rapporto tra grandezze fisiche su scala logaritmica, più precisamente, la sua definizione è:
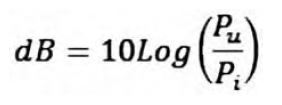
Ricordando alcune proprietà dei logaritmi possiamo affermare che:
- se la potenza di uscita è più grande di quella in ingresso, cioè Pu > Pi (amplificazione) allora avremo che Pu/Pi > 1 e il corrispondente valore in dB sarà positivo
- se la potenza di uscita è più piccola di quella in ingresso, cioè Pu < Pi (attenuazione) allora avremo che Pu/Pi < 1 e il corrispondente valore in dB sarà negativo (il logaritmo di un numero minore di 1 è negativo)
- se la potenza di uscita è esattamente uguale a quella in ingresso, cioè Pu = Pi, allora il sistema né amplifica né attenua, Pu/Pi = 1 e il corrispondente valore in dB sarà nullo (il logaritmo di 1 è uguale a 0)
Precisiamo che i termini positivo e negativo si riferiscono al risultato della formula in cui il rapporto è Pu/Pi. Possiamo anche dire che questa formula indica il guadagno (in termini generali) del sistema e quindi guadagno positivo significa amplificazione, guadagno negativo significa attenuazione, guadagno zero, infine, indica un comportamento assolutamente neutro.
Attenzione ad usare correttamente la terminologia! Se, per esempio, sto valutando il comportamento di una tratta in fibra ottica, il risultato della formula (come l’abbiamo considerata) è negativo (per esempio: -5 dB) ad indicare che il sistema attenua; In questo caso devo dire che il sistema presenta un guadagno di -5 dB, oppure posso dire che presenta un guadagno negativo di 5 dB o, ancora che presenta un’attenuazione di 5 dB. Non devo assolutamente cadere nell’errore di dire che il cavo presenta un’attenuazione di -5 dB perché un’attenuazione negativa equivale ad un guadagno positivo. In altre parole, il termine “attenuazione” contiene già il concetto di perdita e non deve essere ribadito mettendo il segno meno davanti al numero.
Per prendere confidenza con questa scala, analizziamo ora alcuni casi particolari. Supponiamo che il nostro sistema abbia un guadagno positivo di 100, cioè la potenza (elettrica, per esempio) in uscita sia 100 volte quella in ingresso, quanto vale il guadagno in dB? Applichiamo la formula:

Ricordiamo che il logaritmo di un numero è l’esponente che deve essere dato alla base (nel nostro caso 10) per ottenere quel numero. Quindi Log(100) = 2 e la nostra formula diventa:
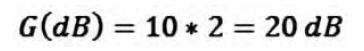
Quindi un sistema che amplifica la potenza di ingresso di 100 volte guadagna 20 dB; analogamente potremmo verificare che un rapporto Pu/Pi = 1000 corrisponde a 30dB; Pu/Pi = 10.000 corrisponde a 40dB, e così via.
Analogamente per quanto riguarda le perdite. Un sistema che attenua il segnale di ingresso di 1000 volte perde 30 dB, un sistema che lascia passare solo lo 0,000001% del segnale di ingresso attenua di 100.000.000 volte e quindi perde 80 dB, ecc., Tabella 1.
Un altro caso particolare e molto utile quando si tratta di fare conti in questo contesto è rappresentato del guadagno o perdita di un fattore 2. Se, cioè, il rapporto Pu/Pi = 2 (oppure ½) si ha che

oppure
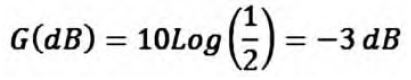
Se abbiamo un cavo in fibra ottica multimodale lungo, per esempio, 1,5 km, e che attenua (a 850nm) 3 dB, significa che qualunque sia il valore dell’energia luminosa in ingresso, in uscita questo valore sarà dimezzato.
Dalle proprietà dei logaritmi deriva un altro grande vantaggio dell’operare con i decibel. Supponiamo di voler calcolare il comportamento di un sistema complesso, cioè costituito da una serie di elementi in cascata di cui conosciamo (o possiamo misurare) il comportamento individuale. Una tipica situazione è rappresentata in Figura 3.

Figura 3 – Sistema di trasmissione su una linea di trasmissione amplificata
Gli elementi della catena possono essere tratte di cavo, connettori o anche circuiti amplificatori del segnale. Per ogni elemento è indicato il valore di guadagno (o di perdita). Se questi valori sono espressi in decibel per conoscere il comportamento dell’intera catena è sufficiente eseguire la semplice somma algebrica dei valori parziali, nel nostro esempio:
(-3)+(-18)+(23)+(-16)+(-3) = -17 dB
L’intero sistema quindi attenua il segnale della sorgente di 17 dB. Un’informazione certamente utile, ma mettiamola in pratica: riusciamo a calcolare quanto vale il segnale di uscita a fronte di un segnale di ingresso ben preciso, per esempio 1W? Se avete seguito con attenzione quanto è stato detto finora avete tutti gli elementi per calcolarlo.
Abbiamo visto alcuni casi particolari: nella Tabella 1 c’è il valore 10, 20, 30, 3 ma il valore 17 dB non c’è. Certamente significa attenuazione minore di 100 volte ma quanto esattamente?
Per risolvere il problema basta scomporre questo valore in una catena di due (o più) elementi semplici e noti che danno per totale -17 dB, per esempio
– 20 dB + 3 dB = – 17 dB
È come se il nostro segnale attraversasse due elementi in cascata, il primo attenua di 20 dB (attenuazione di un fattore 100) e il secondo amplifica di 3 dB (raddoppio). Ora è facile: il primo elemento lascia passare solo 1/100 del segnale, il secondo raddoppia il valore del segnale, quindi dimezza la perdita, in totale quindi risulta un’attenuazione di 50 volte; se il segnale di ingresso vale, come abbiamo ipotizzato, 1W, in uscita troverò i 2/100 di questo valore, cioè 0,02W che posso esprimere anche come 20 mW.
Ora siamo in grado anche di rispondere alle due domande contenute nell’introduzione a queste note: in entrambi i casi l’attenuazione di un cavo è esattamente la metà dell’altro; il cavo che attenua 30 dB attenua di 1000 volte il segnale di ingresso, mentre tra i due cavi da 25 dB e da 28 dB la differenza è esattamente 3 dB, (28 =25 + 3) vuol dire che dopo aver introdotto la stessa attenuazione dell’altro, il cavo da 28 dB introduce un ulteriore dimezzamento del segnale.
Capito il meccanismo rispondete (da soli) a quest’ultima domanda molto facile: Sempre nell’ipotesi di segnale in ingresso di 1W, quale sarà il valore in uscita da un sistema che attenua 15 dB?
Il dBm
Dagli esempi analizzati è evidente che se mi interessa conoscere il valore del segnale in uscita è necessario che risalga al valore di guadagno globale del sistema per applicarlo al segnale di ingresso, cioè devo riconvertire il dato in dB in un dato lineare. Questa operazione può essere anche complessa ed elimina molti dei vantaggi legati all’utilizzo di una scala logaritmica. È certamente più conveniente eseguire l’operazione opposta, cioè convertire in dB anche il valore dei segnali in ingresso e in uscita.
Il decibel, per come è stato definito, può rappresentare solo il valore del rapporto tra due grandezze, non una grandezza in valore assoluto, non posso, cioè, utilizzarlo per rappresentare un valore preciso di energia, di potenza, di corrente, di tensione, ecc., a meno che non si ricorra all’espediente di rapportare questa grandezza ad un riferimento fisso e generalmente condiviso. Nel caso più frequente e più interessante per noi, si può esprimere in decibel il valore in Watt (o nei suoi sottomultipli) di una sorgente, come rapporto con il valore fisso di riferimento di 1 mW. Cioè, se P è la potenza associata alla fonte di energia, in decibel si esprimerà come:

Una sorgente di 1W (che equivale a 1000 mW) si esprimerà come
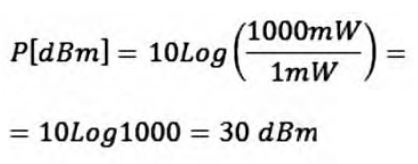
Quindi 1W = 30 dBm; il simbolo dBm sta ad indicare che si tratta del valore di una potenza riferita ad 1mW.
In base a quello che sappiamo già possiamo costruire i seguenti esempi:
- 9 dBm = 8 mW ( 9 = 3+3+3, quindi tre raddoppi consecutivi del valore di riferimento 1 mW)
- 40 dBm = 10 W ( 10.000 volte il valore di riferimento)
- 53 dBm = 200 W (50 + 3; 50 = 100 volte, 3 = raddoppio)
- 0 dBm = 1 mW
- -10 dBm = 0,1 mW
- -20 dBm = 0,01 mW
- Ecc.
Ritorniamo all’esempio di Figura 3, la catena di collegamento tra sorgente e utilizzatore, come abbiamo visto, attenua di 17 dB, e, nell’ipotesi di avere una potenza in ingresso (la sorgente) di 1W, abbiamo calcolato che il segnale in arrivo (sull’utilizzatore) è di 20 mW. Il calcolo sarebbe stato molto più semplice se anche il valore della sorgente fosse stato espresso in dB (più precisamente in dBm). Tenendo conto, infatti, che 1W equivale a 30 dBm, possiamo immediatamente calcolare l’energia in arrivo all’utilizzatore:
30 dBm – 17 dB = 13 dBm
Facciamo notare (solo per scopi didattici) che 13 dBm corrispondono esattamente a quei 20 mW calcolati in altro modo, ma se tutto il sistema, compreso le specifiche della sorgente e dell’utilizzatore, è espresso in decibel, non è necessario quasi mai eseguire queste conversioni.
Esempi di applicazione del dB nei sistemi per il trasporto dell’informazione
Cablaggio in rame
Nella realizzazione di un sistema di cablaggio in rame, incontriamo i decibel solo nella fase di test, tutti i parametri elettrici da misurare e da certificare sono espressi in dB. Il concetto dovrebbe essere ora abbastanza chiaro per quanto riguarda il parametro Insertion Loss, cioè l’attenuazione; è bene comunque chiarire che cosa significano i valori in dB che rappresentano i parametri di diafonia. I parametri NEXT, FEXT, ecc., sono indicati come rapporto tra il segnale che genera il disturbo e il disturbo stesso. Definito in questo modo il risultato (in dB) è sempre positivo e, più è alto il valore ottenuto, minore sarà il disturbo a parità di segnale disturbante. Gli standard danno per ogni categoria di collegamento e per ogni configurazione di misura i valori minimi che devono essere ottenuti su ogni parametro e per ogni frequenza. Per esempio, sul parametro NEXT, il valore minimo che deve essere garantito a 250MHz nella configurazione di canale in Classe E è di 33,1 dB (ISO 11801), significa che il disturbo non può essere superiore ad 1/2000 del segnale disturbante cioè 0,05% (dal punto di vista energetico). Lo stesso standard, per la medesima configurazione impone che a 50 MHz il limite da non superare sia di 45 dB: ciò significa che il disturbo non può essere superiore a 1/32.000 del segnale disturbante ovvero lo 0.003% circa. In Figura 4 è riportato il grafico di una misura sul parametro NEXT di un link in configurazione Channel. La curva rossa rappresenta il limite imposto dallo standard ISO 11801 nel campo di frequenze 1-250 MHz; si può notare che le misure effettuate si mantengono sempre al di sopra della curva limite tranne in un punto in cui il disturbo su una coppia è troppo alto e fa fallire la certificazione. Non abbiamo riportato i dettagli perché esulerebbero dagli scopi di queste note, comunque, come si può dedurre anche da un’attenta analisi del grafico, la misura che fa fallire la certificazione supera il limite ‘soltanto’ per 3 dB, il che corrisponde a un disturbo rilevato che è il doppio rispetto a quanto ammesso dalle normative a quella frequenza (sempre da un punto di vista energetico).
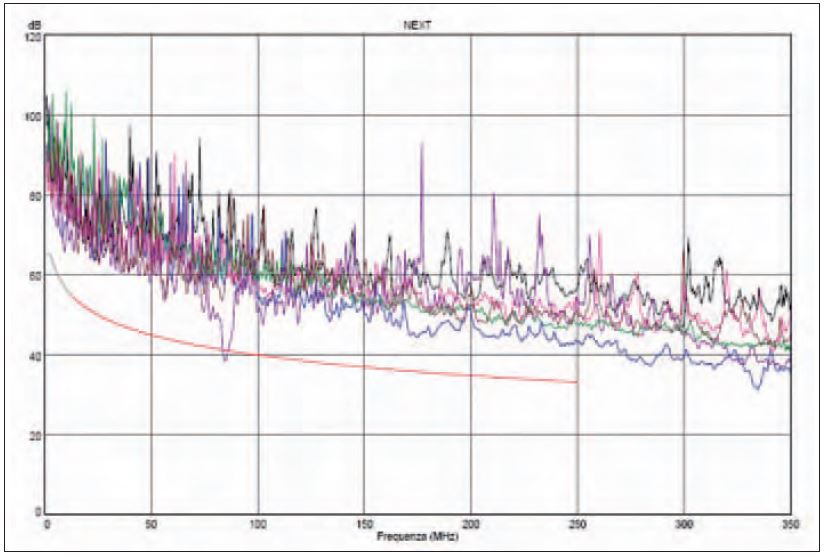
Figura 4 – Tracciato della misurazione dell’attenuazione di NEXT su un collegamento in Cat.6 / Classe E
Sistemi in fibra ottica
Nel campo dei sistemi in fibra ottica di nostro interesse, la misura più significativa è quella di attenuazione. La misura dell’attenuazione di un link ottico si effettua con la tecnica della doppia misura: si misura il valore di una sorgente di energia luminosa e poi si ripete la misura interponendo il link da valutare. Se la misura dell’energia luminosa in un caso e nell’altro è espressa in dBm, la differenza tra le due letture rappresenta l’attenuazione (in dB) dell’intero collegamento ottico sotto esame. La Figura 5 mostra lo schermo di uno strumento molto diffuso dopo aver effettuato la misura della sorgente luminosa (questa fase si chiama anche impostazione del riferimento). Come si può vedere il valore della sorgente di energia (può variare in un campo relativamente ampio) è, in questo caso, intorno ai -20 dBm. Come dovrei comportarmi se volessi esprimerla in Watt?
Per prima cosa ricordiamo che qui le potenze sono espresse come rapporto rispetto a 1mW, quindi questa energia è circa 20 dB al di sotto di 1mW o, in altre parole (siccome -20 dB significa 1/100), vale all’incirca 0,01mW cioè 10 µW.
Ricordiamo anche che, quando si misura l’attenuazione di un collegamento ottico, il limite di riferimento non è fisso, come accade per i sistemi in rame, ma dipende dalla configurazione del link. È compito del tecnico che certifica (anche se molti strumenti automatici possono aiutare in questa fase) calcolare il limite con cui confrontare le misure effettuate semplicemente sommando le attenuazioni massime permesse (in dB) degli elementi che compongono il collegamento (per esempio: 350 m di fibra multimodale + 1 giunzione + 2 connettori, con segnale a 850 nm). Lo standard ISO 11801 indica come valori massimi di attenuazione per questi elementi:
Fibra 3,50 dB/km
Giunzione 0,30 dB
Connettore 0,75 dB
Il limite per il link descritto è pertanto: 1,22 dB (fibra) + 0,3 dB (giunzione) + 1,5 dB (connettori) = 3,02 dB.
La semplicità con cui si calcola il limite totale è dovuta esclusivamente all’utilizzo dei decibel.

Figura 5 – Impostazione del riferimento per una misura di attenuazione su collegamento ottico
Sistemi radio
Per concludere gli esempi di calcolo con i decibel prendiamo in considerazione il dimensionamento di un collegamento wireless. È un caso particolarmente interessante perché gli elementi della catena di trasmissione dal trasmettitore al ricevitore pur essendo tutti passivi, apportano un contributo sia positivo che negativo al bilancio di attenuazione.

Figura 6 – Sistema di trasmissione su collegamento wireless
Analizziamo la Figura 6, abbiamo un trasmettitore A che emetterà un segnale RF (radio frequenza) caratterizzato da una determinata frequenza (la banda su cui vogliamo lavorare, per esempio 2,4 GHz) e da una potenza di uscita che solitamente è regolabile. Gli altri elementi che abbiamo incluso sono il cavo di collegamento B, l’antenna C, il percorso “in aria” D, la seconda antenna E, il cavo F ed il ricevitore G. Supponiamo che i valori di attenuazione/guadagno dei componenti per questo link radio siano:
A – Trasmettitore, con una potenza di uscita di 7 dBm
B – Cavo di collegamento, perdita di 1 dB (inclusi i connettori)
C – Antenna trasmittente, guadagno 17 dBi
D – Percorso in aria. Supponendo la distanza = 5 km l’attenuazione è di 114,21 dB (@ 2,4 GHz)
E – Antenna ricevente, come C, guadagno di 17 dBi
F – Cavo di collegamento, perdita di 1 dB (inclusi i connettori)
G – Apparato ricevente. Sensibilità di ingresso = -76 dBm
L’antenna presenta un guadagno positivo, si comporta come se amplificasse il segnale. Questa caratteristica è dovuta al fatto che nessuna antenna è perfettamente isotropica, non emette cioè in modo uniforme in tutte le direzioni dello spazio. Questo effetto è, quasi sempre, voluto perché in ogni applicazione esistono direzioni in cui non mi interessa o, addirittura, si vuole evitare di trasmettere energia. Le antenne direzionali, come quella ipotizzata nel nostro esempio, poi, concentrano tutta l’energia RF ricevuta dal trasmettitore in una sola direzione privilegiata, pertanto, rispetto all’antenna isotropica evidenziano un guadagno tanto più alto quanto più sono direzionali, cioè quanto più stretto è il fascio di emissione. Per rappresentare il guadagno di un’antenna si usa il simbolo dBi che non è altro che la misura in decibel del rapporto tra l’intensità del campo radio (misurato nella direzione di emissione) rapportato a quello che si avrebbe, nella stessa direzione, con un’antenna isotropica.
Supponiamo ora di dover valutare la fattibilità di un tale collegamento; per prima cosa dobbiamo valutare quanta energia arriva al connettore del ricevitore. È sufficiente eseguire una semplice somma algebrica inserendo ogni contributo con il proprio segno. Quindi:
7 dBm – 1 dB + 17 dBi – 114,21 dB + 17 dBi – 1dB = – 75,21 dBm
Siamo partiti dalla potenza emessa dal trasmettitore (in dBm) e dopo aver applicato i fattori di perdita e di guadagno lungo tutto lo sviluppo del percorso del segnale abbiamo calcolato la potenza residua che arriva all’apparato ricevente.
Per valutare se questo collegamento è fattibile basta confrontare quest’ultimo valore con la “sensibilità di ingresso” del nostro ricevitore. La sensibilità di ingresso del ricevitore è un dato rilevabile dalle specifiche di prodotto ed indica il valore della potenza RF minima che deve giungere all’apparato perché questi riesca a funzionare correttamente, anche questo valore è sempre indicato in dBm.
L’apparato scelto per questo esempio ha una sensibilità di ingresso di -76 dBm, quindi questo ponte radio su 5 km, può funzionare.
Peccato che sia fuori legge!! Sulla banda dei 2,4 GHz, infatti la potenza emessa dall’antenna, in qualunque direzione, non può superare i 20 dBm (100 mW), e se andiamo a calcolare la potenza emessa dall’antenna, cioè l’energia RF subito dopo l’antenna trasmittente abbiamo:
7 dBm – 1 dB + 17 dBi = 23 dBm
esattamente il doppio di quanto la legge prescrive come massimo!!
Lavorare con i decibel ci permette di trovare agevolmente la soluzione, basta, per esempio, cambiare l’antenna con una a guadagno maggiore (21 dBi) e regolare il trasmettitore su una potenza di emissione più bassa. Quindi:
0 dBm – 1 dB + 21 dBi – 114,21 dB + 21 dBi – 1dB = – 74,21 dBm
Ora tutti i requisiti sono soddisfatti. Attenzione, non lasciamoci ingannare da quella regolazione del trasmettitore a 0 dBm, ricordo che non vuol dire che la potenza di emissione sia nulla ma, e ormai dovreste saperlo bene, esattamente 1 mW.
Un’ultima considerazione sulla sensibilità di ingresso di – 76 dBm, calcoliamo, per curiosità e anche per fare un ultimo esercizio, quanto vale in W. Possiamo scrivere questo valore anche come:
– 76 dBm = – 70 dB – 3 dB – 3 dB quindi:
-76 dBm = 1/10.000.000 x ½ x ½ cioè
1/40.000.000 mW = 1/40.000.000.000 W
Un quarantamiliardesimo di Watt !!! Non lamentiamoci troppo se gli apparati WiFi migliori costano un po’ più degli altri …
Conclusioni
L’utilizzo delle scale logaritmiche permette di gestire agevolmente valori molto grandi e/o molto piccoli e consente di determinare il comportamento di sistemi anche molto complessi con una serie di operazioni elementari. Tuttavia è importantissimo avere sempre la consapevolezza di quello che si sta misurando o valutando. Queste brevi note, scritte con l’obiettivo di introdurre il lettore ai ‘misteri del decibel’, spero abbiano raggiunto lo scopo di rendere facilmente fruibili, nella pratica delle attività tecniche quotidiane, le informazioni espresse con questa unità di misura e agevole l’impiego del dB nella progettazione, nell’analisi, nella verifica e nella risoluzione di problemi relativi ai sistemi di trasporto dell’informazione.

